A Dangerous Maze : Solution
বোঝার সুবিধার্থে, Positive মানের দরজা গুলোকে কালো দরজা এবং Negative মানের দরজা গুলোকে নীল দরজা ধরলাম।
ধরি, তোমার কাছে ৫ টি দরজা আছে। কালো দরজা দিয়ে তুমি বের হতে পারবে আর নীল দরজা দিয়ে তুমি আবার Maze এ ফিরত আসবে।
যদি কালো দরজা Choose করো তাহলে কালো দরজার গায়ে লেখা সময় পর তুমি Maze থেকে বের হতে পারবে আর যদি নীল দরজা Choose করো তাহলে নীল দরজার গায়ে লেখা সময় পর তুমি আবার Maze এ ফিরে আসবে।
আমাদের বের করতে হবে Expected কত সময় পর তুমি Maze হতে বের হবে??
ধরি, এই Expected সময় হচ্ছে E,
মোট দরজার সংখ্যা = ৫
যে কোনো একটি দরজা Choose করার Probability = ১/৫
যদি নীল দরজা Choose করো তাহলে দরজার গায়ে লেখা ঐ সময় পর আবার Maze এ ফিরে আসবে, এর ফলে তোমার ঐ সময় টা নষ্ট হবে এবং তোমার Maze থেকে বের হবার Expected সময়ের মানের কোনো Change হবে না।
তাহলে আমরা লিখতে পারি,
E = (1/5)*5 + (1/5)*2 + (1/5)*(7+E) + (1/5)*3 + (1/5)*(4+E)
E = (1/5)*(5 + 2 + 7 + 3 + 4) + (1/5)*2E
E - (1/5)*2E = 21/5
E * (1 - 2/5) = 21/5
E * 3/5 = 21/5
E = 7
সুতরাং উপরের Problem টার জন্য Expected সময় হলো ৭.
আবার ধরি,
n = মোট দরজার সংখ্যা
C = যত গুলা দরজা Choose করলে আমি আবার Maze এ ফিরত আসবো তার সংখ্যা
T = প্রত্যেকটি দরজার জন্য দেওয়া সময়
E = Expected সময়
তাহলে আমরা Expected সময়কে লিখতে পারি,
E = (1/n)*(∑T + C*E)
E = (1/n)*∑T + (1/n)*C*E
E * (1 - C/n) = (1/n)*∑T
E * (n - C)/n = (1/n)*∑T
E = n/(n - C) * (1/n)*∑T
E = ∑T/(n - c)
Coding Part :
#include<bits/stdc++.h>
using namespace std;
int main()
{
int t, k = 1;
cin >> t;
while(t--)
{
int n;
cin >> n;
int sum = 0, a, negative_flag = 0;
for(int i=1; i<=n; i++)
{
cin >> a;
if(a < 0)
{
negative_flag++;
a = a*(-1);
}
sum += a;
}
cout << "Case " << k++ << ": ";
if(n == negative_flag)
cout << "inf" << "\n";
else
{
int gcd = __gcd(sum, n-negative_flag);
cout << sum/gcd << "/" << (n - negative_flag)/gcd << "\n";
}
}
return 0;
}
বিঃ দ্রঃ GCD দ্বারা ভাগ দেওয়ার কারণ Output format দেখতে p/q এর মতো। সে জন্য q যাতে p এর Divisor হয়।
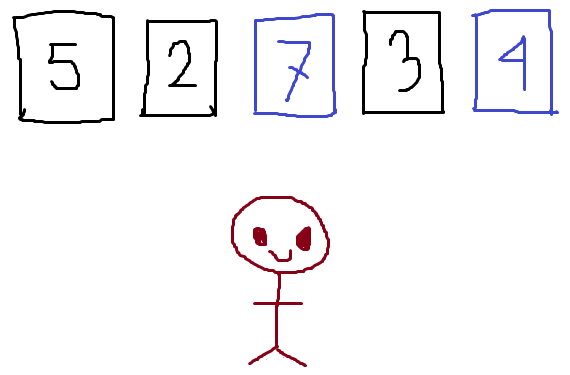
Comments
Post a Comment